Calculating your sample size

During the course of your market research, you may be unable to reach the entire population you want to gather data about. While larger sample sizes bring you closer to a 1:1 representation of your target population, working with them can be time-consuming, expensive, and inconvenient. However, small samples risk yielding results that aren’t representative of the target population. 

Luckily, you can easily identify an ideal subset that represents the population and produces strong, statistically significant results that don’t gobble up all of your resources. In this article, we'll teach how to calculate sample size with a margin of error to identify that subset.

Five steps to finding your sample size

1. Define population size or number of people
2. Designate your margin of error
3. Determine your confidence level
4. Predict expected variance
5. Finalize your sample size

Follow these five steps to ensure you get the right selection size for your research needs.

Download: The State of AI in Market Research

Define the size of your population

Your sample size needs will differ depending on the true population size or the total number of people you’re looking to conclude on. That’s why determining the minimum number of individuals required to represent your selection is an important first step.

Defining the size of your population can be easier said than done. While there is a lot of population data available, you may be targeting a complex population or for which no reliable data currently exists. 

Knowing the size of your population is more important when dealing with relatively small, easy-to-measure groups of people. If you’re dealing with a larger population, take your best estimate, and roll with it. 

This is the first step in a sample size formula, yielding more accurate results than a simple estimate – and accurately reflecting the population.

Designate your margin of error

Random sample errors are inevitable whenever you’re using a subset of your total population. Be confident that your results are accurate by designating how much error you intend to permit: that’s your margin of error.

Sometimes called a "confidence interval," a margin of error indicates how much you’re willing for your sample mean to differ from your population mean. It’s often expressed alongside statistics as a plus-minus (±) figure, indicating a range which you can be relatively certain about. 

For example, say you take a sample proportion of your colleagues with a designated 3% margin of error and find that 65% of your office uses some form of voice recognition technology at home. If you were to ask your entire office, you could be sure that in reality, as low as 62% and as high as 68% might use some form of voice recognition technology at home.

Determine how confident you can be

Your confidence level reveals how certain you can be that the true proportion of the total population would pick an answer within a particular range. The most common confidence levels are 90%, 95%, and 99%. Researchers most often employ a 95% confidence level.

Don’t confuse confidence levels for confidence intervals (i.e., mean of error). Remember the distinction by thinking about how the concepts relate to each other to sample more confidently.

In our example from the previous step, when you put confidence levels and intervals together, you can say you’re 95% certain that the true percentage of your colleagues who use voice recognition technology at home is within ± three percentage points from the sample mean of 65%, or between 62% and 68%.

Your confidence level corresponds to something called a "z-score." A z-score is a value that indicates the placement of your raw score (meaning the percent of your confidence level) in any number of standard deviations below or above the population mean.

Z-scores for the most common confidence intervals are:

• 90% = 2.576
• 95% = 1.96
• 99% = 2.576

If you’re using a different confidence interval, use this z-score table to find the correct value for your calculation.

Decide the variance you expect

The last thing you’ll want to consider when calculating your sample size is the amount of variance you expect to see among participant responses. 

Standard deviation measures how much individual sample data points deviate from the average population. 

Don’t know how much variance to expect? Use the standard deviation of 0.5 to make sure your group is large enough. 

Read: Best Practices for Writing Discussion Guides (eBook)

Finding your ideal sample size

Now that you know what goes into determining sample size, you can calculate sample size online. Or, calculate it the old-fashioned way: by hand. 

Below, find two sample size calculations - one for the known population proportion and one for the unknown population.

Sample size for known population

Sample size for unknown population

Here’s how the calculations work out for our voice recognition technology example in an office of 500 people, with a 95% confidence level and 5% margin of error:

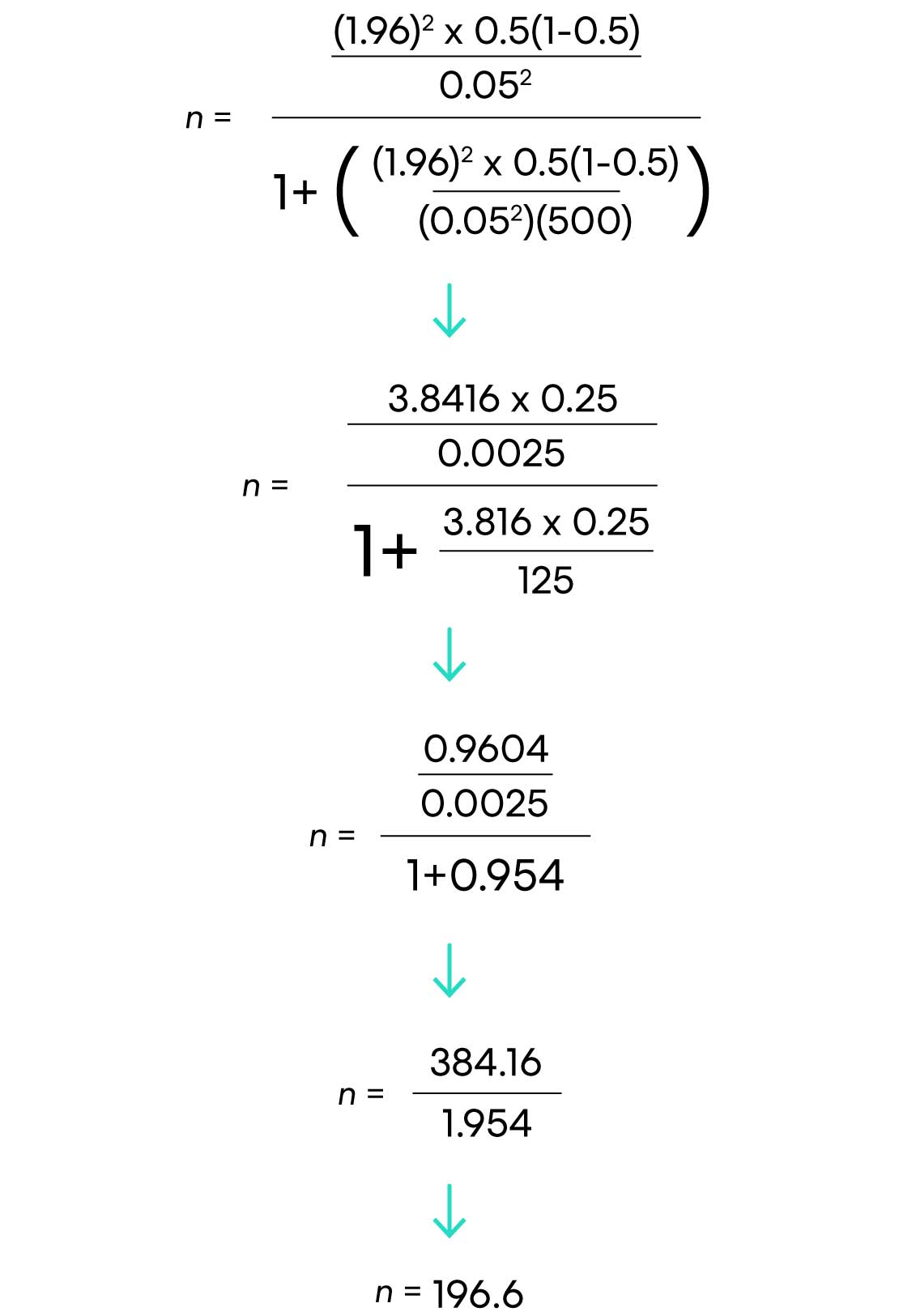
There you have it! 197 respondents are needed.

You can tweak some things if that number is too big to swallow.

Try increasing your margin of error or decreasing your confidence level which will reduce the number of respondents necessary but increase chances for errors.

Summing Up Sample Size

Calculating sample size sounds complicated - but, utilizing an easy sample size formula and even calculators are now available to make this tedious part of research faster!

Now, it's time to recruit your sample and run a focus group or even a customer satisfaction survey. Whatever you decide, you now have the information needed to make decisions with confidence.

Want to whip your research skills into shape? Check out our go-to eBook on writing discussion guides!

‍